How Bitcoin Works
How Bitcoin Works: A Guide for the Digitally Perplexed1 #
This article was highlighted in the Boston Globe in 2014.
Suddenly in 2013, the word was everywhere: sometimes as “Bitcoin”, sometimes belittled as merely “bitcoin”. Bitcoin was used to buy a $130,000 luxury car, praised in solemn US Congressional committee hearings, but banned in China even as ATMs for it spread around the world. Its price on unregulated exchanges soared and plummeted wildly, from almost nothing to over $1,000 a coin.
The number of businesses and institutions that accepted Bitcoin surged, but nobody seemed to know whether the new currency was headed for an ignominious crash and oblivion, or whether instead it would be remembered as one of the defining inventions of the twenty-first century.
Here is how it works.
Beginnings #
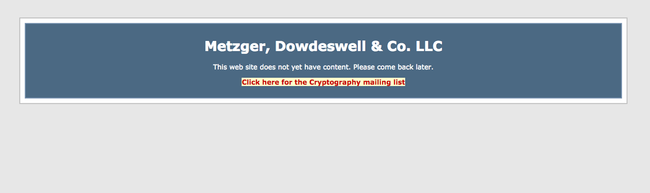
At the website where everything began, time stands still. It has the feel of a ghost-town in a Western movie, desolate and abandoned, with only the occasional tumbleweed or dust devil drifting by. At the top of the page is the name of a small New York City computer security firm. Underneath, some unstyled text reads: “This website does not yet have content. Please come back later.”, but the page hasn’t changed in years.2 Beneath, there is a link, “Click here for the Cryptography mailing list”. Below that, just empty space.
Subscriptions to the mailing list are handled automatically. Anyone can join, but the overall sense of neglect helps ensure that only specialists and the cryptographic cognoscenti ever actually sign up. Traffic is generally light, and, in 2008, October ended as slowly as it had begun. A little after five in the afternoon, someone posted a message with the abstruse subject heading, “Who cares about side-channel attacks?” Apparently nobody; no-one posted anything else that Friday, and the month finished with an average of less than two posts a day.
For the rest of the world, October had not been so quiet. On October 1st the Dow Jones Index had begun its descent towards terrifying lows. On the 15th, it set a new record, dropping 733 points in a single day. Economies around the world plunged into the worst financial crisis since the Great Depression of 1929.3 But as October drew to a close with the old financial system in ruins, a new one slipped softly into the world on the cryptography mailing list.
If you had clicked the list’s link that Friday night, and aimlessly clicked on the few links behind it, you would have stumbled onto the second-to-last post of the day.4 It was sent a few hours before the ignored side-channel attack message, by one Satoshi Nakamoto. This was his first post to the list,5 and no one there had ever heard of him before. Satoshi Nakamoto would turn out to be a pseudonym, and when he (or she, or they) faded from sight a few years later, his identity still remained a mystery.6
Satoshi’s email was short enough to read without having to scroll, and it contained a link to a short PDF he had written. To stretch it to eight pages he had used enormous margins, and his references took up less than half of the ninth and last page. It was written in deceptively plain and lucid English; despite his Japanese name, Satoshi was clearly a native English speaker.
With nothing better to do, you might have begun to read; and, despite the cryptography jargon, you would have realized that this was a guileless proposal for a world currency. It would not belong to any government, or to any country. It would not depend on gold or silver for its value. It would not be backed, or even controlled, by any nationally or internationally recognized organization or corporation, let alone a bank or any other financial institution. It would be a new form of money that could not be seen or heard or touched, created by computer code that Satoshi had not yet finished.
It all seemed, hopelessly, even romantically, utopian, like a proposal for a new Esperanto or to organize a movement to rid the world of nuclear weapons. Most likely, after reading Satoshi’s PDF, you would have shaken your head sadly at the crackpots that haunt the remote and isolated back-alleys of the Internet; quietly shut down your computer; and shuffled off to bed.
We don’t know why Satoshi announced his idea on the cryptography mailing list, or what he was looking for from the list’s members. What he got was a flurry of comments and questions that lasted a month, and then everyone lost interest. Or, almost everyone: a very few followed Satoshi to a different website - for programmers only - and helped him write and test his developing computer code.
An initial version was running on the Internet by early 2009. Over the next few years, word of Satoshi’s odd digital money spread slowly among Internet programmers. In 2011, it spilled over into the mainstream media with an article in Time magazine.7 In January 2013, a single bitcoin cost around $12. In November, the price suddenly started shooting up, and on the 28th it passed $1,000.8 By December, more people were Googling Bitcoin than Miley Cyrus’ hit song Like a Wrecking Ball.91011 The heat of the exploding media coverage was intense, but it generated no light: how Bitcoin worked remained baffling to most everyone.
Bitcoin is new kind of money. But more important is its dramatic demonstration that trust and honesty can exist reliably in a social network, without any centralized enforcement, even if everyone in the network is determined to steal from everyone else. Bitcoin has changed how people will think think about trust forever.
Here is how it works.
The Bank #
Imagine we are going to start a bank. We’ll just call it the Bank, with a capital B. The Bank will have offices, tellers, debit cards, checks, everything a modern bank has. We will convince our friends and relatives to open checking and savings accounts, and then use their money to provide mortgages, car loans, and other forms of lending to make a profit.12
We will have to keep track of all the money going in and out of the Bank, and we’ll do that with a single, very large ledger. Let’s simply call it the Ledger, with a capital L. Every time someone makes a deposit to the Bank we will enter it in the Ledger as a credit, and every time we make a loan or a depositor withdraws cash, we’ll record this as a debit. At any one time, we can always look at the last line of the Ledger, and know exactly how much money the Bank has.
Eventually, of course, we will take the Bank online. Imagine, now, that we do something a little odd. On the Bank’s web site, we publish our Ledger online for everyone to see. If Alice, one of our account holders, offers to buy something from Bob for $10,000 with a check, Bob can go to the Bank’s website, look at the Ledger, and see whether Alice actually has enough money in her account to cover the check.
In the real world, Alice doesn’t want every Tom, Dick, and Bob to be able to see her account and every transaction she has ever made. Instead, she wants the Bank to just tell Bob whether the check will clear, and she’s willing to pay the Bank a fee for that service.
But that’s beside the point. The point is that, any bank is essentially just a Ledger, recording every transaction in and out of its accounts. It doesn’t matter how much gold a bank has in its vaults, or how many account holders it can boast, or how opulent its lobby is. The Ledger tells us how much money the bank really has, as well as how much any of its account holders has at any one time.
This will become important later. For now, let us just agree that it is an interesting fact that wasn’t immediately obvious, and set it to one side.
The Game #
Now, let’s try to imagine something more ambitious: an entire digital online world! This world will have a geography, with mountains, rivers, and oceans; cities and villages, crops and factories, wizards and warriors, and farmers; horses, ships, even dragons, and talking animals and birds. Why not? This is a fantasy world in which real people adopt an online persona. On the Internet, nobody knows you’re a dog; in our world, nobody knows who you really are, whether you are a man or a woman or a child, or even playing more than one persona.
I say “playing”, because what we are talking about here is an online game. Actual games similar to this exist on the Internet, with names like World of Warcraft, or Second Life. Players typically have strange names like Wrathion or Warlock, or evilclown23. Epic digital battles are fought and lost, vast conspiracies hatched and foiled, industrial and military empires created and destroyed. Our online world will be this kind of game. We shall call it simply: the Game.
Anyone who wishes to play in the Game may simply join it; if they don’t, they don’t. The Game will just be there, online, and it will cost nothing to join. It will only exist to the extent that people are actually in it. The Game is an organization, a network.
But the Game will differ in one important way from other games: the Game will have no center. There will be no there there. What does this mean?
Consider a global, influential organization like the Catholic Church. With over one billion members, it has a geographical center - the Vatican in Rome - and a single chief representative, the Pope. It is possible to take legal action against the Catholic Church: you can sue the Holy See. There is a there there.
By contrast, you cannot sue the Protestant Church, or Buddhism, or Islam. Even more Muslims share the same essential faith than do Catholics, but there is no final arbiter of Islamic doctrine as there is a Pope. For example, when decisive religious edicts (fatwas) on Islamic religious law or doctrine are issued, they come from leading religious clerics. But how clerics are appointed and authorized differs by country, denomination, and even from one region or community to the next. There is no one central Islamic authority. You cannot sue Buddhism or Sunni Islam any more than you can sue the human race. No matter how great and powerful these organizations are, in this special sense, there is no there there.
Our Game will be like this. It will have no central computer or “server” where players sign up; no commercial company or government or centralized authority will run it or maintain it. If you wish to join the Game, you find a copy of the Game program somewhere, on the Internet or a store; it doesn’t matter where. You run it on your computer, and connect to the Internet. Any Game program will be able to find other running Game programs, and connect to them. The Game will be a network.
Computer programs of this kind already exist. A famous example is Bittorrent. With Bittorrent, there is no there there. You simply find a copy of the program, run it on your computer, and voilá: it will display other Bittorrent programs running on the Internet. To download a movie from any of them, you double-click it. Instead of a single Bittorrent server sending you this very large file, which would take a long time, all the Bittorrent servers on the network which have a copy of the movie collaborate, and each sends you a little piece of the movie – a different piece. Downloading a hundred pieces of a movie from a hundred different servers is much faster than downloading it in one piece from a single server.13 Once it has been downloaded to you, your Bittorrent server will be able to collaborate and send small pieces to anyone else on the Internet as well.
You cannot sue Bittorrent. There are no Bittorrent kingpins, no Bittorrent organization, no one company that makes the software, no central server. Everything is everywhere and nowhere. Bittorrent servers are constantly appearing and disappearing, like waves in the ocean. There is no there there; it just is.14
This is how our Game will function. If a character named Wrathion is created on one Game server, that server will share this fact with all the other Game servers that are running. In the Game, every breath you take and every move you make, every bond you break and every step you take, will be broadcast, to everyone. The Game will play on and on.
The Money #
We will, of course, want the Game to have money. The Game will have to have its own currency; call it the Coin.
If the Game were centralized, implementing money would be straightforward. Just as there would be a central Game server, so there would be a central Bank for the Game. Every player would have an account with it. For Alice to pay Bob, Alice would simply transfer Coins from her account to Bob’s. Simple.
But the Game is not centralized. It cannot rely on a central Bank that could disappear at any moment, taking everyone’s money with it. Just as the names of the Game’s players, like Wrathion and evilclown23, must be on all the Game servers everywhere, so must the money.
And that means anyone playing the Game can also try to steal other players’ Coins. The heart of the Game is not one central computer somewhere; instead, Game computers can be anywhere on the Internet, and are. Anyone can set up a new Game computer, and try to trick it into stealing Coins.
Our Game’s money problem is not so different from how a world of nation states, all motivated by self-interest, and under the sway of no enforcing power, might, nevertheless, live in peace instead of a perpetual state of war. Even, as Immanuel Kant framed the problem, if the peoples of all these nations are evil demons. Kant proposed a solution in On Perpetual Peace, which crucially required that the demons be not only evil and self-interested, but also rational. Our problem is similar, and seems just as impossible. In a network in which everyone and anyone can be expected to cheat and steal money, if they can get away with it, we need to devise a monetary system that is stable and trusted. In short, a currency for a vast international community that will work without a Hobbesian Leviathan to keep it from tearing itself apart, even if it is peopled entirely with evil demons.
The solution, Satoshi realized, begins with a ledger.
The Ledger #
Instead of a Bank, the Game will have a ledger like the one we made earlier for our Bank: the Ledger. When the Game begins, some very lucky first-time players will start out with money created out of thin air. The Ledger will look something like this:
Figure 1: The Game’s “genesis” players’ Ledger entries #
| Payer | Payee | Amount | Date/Time |
| - | Adam | 1,000,000 | 2008 NOV 1 10:22AM |
| - | Eve | 1,000,000 | 2008 NOV 1 10:22AM |
| - | Cain | 1,000,000 | 2008 NOV 1 10:22AM |
| - | Abel | 1,000,000 | 2008 NOV 1 10:22AM |
The rules of the Game and the Ledger will be that after these “genesis” players, no one else can get money from an “empty” payer. All future entries must have the name of someone in the “Payer” column, and that someone must already exist in the Ledger: they must already have money.
The happy genesis players will start out very rich, of course. But just as in the real world, money isn’t any use unless you can buy something with it. As the Game progresses and more players join, Adam, Eve, Cain, and Abel will start buying things from these new players, and so the money will percolate into the Game and start to reach all the players. The table below shows a Ledger with a first such entry, from Cain to a new player named Alice.
Figure 2: How Coins get into circulation #
| Payer | Payee | Amount | Date/Time |
| - | Adam | 1,000,000 | 2008 NOV 1 10:22AM |
| - | Eve | 1,000,000 | 2008 NOV 1 10:22AM |
| - | Cain | 1,000,000 | 2008 NOV 1 10:22AM |
| - | Abel | 1,000,000 | 2008 NOV 1 10:22AM |
| Cain | Alice | 500 | 2013 DEC 24 9:45PM |
When later Alice wants to buy something from Bob for 100 Coins, Bob can look in the Ledger to see if Alice even owns that many Coins. When he sees that she does, he and Alice will create an entry in the Ledger that looks something like this:
Figure 3: Alice pays Bob 100 Coins #
| Payer | Payee | Amount | Date/Time |
| Alice | Bob | 100 | 2013 DEC 28 7:32PM |
The Game server they do this on will broadcast this change to all the other Game servers on the Internet, and those will all update their local copy of the Ledger accordingly. This may take a few minutes, but not enough to worry about.
Notice that the Game doesn’t have to invent any actual digital coins, or any digital wallets to store them in. There are no “things” to steal; also no bulky cash, no checks, no credit cards. There is not even a bank to maintain or defend. There is only the Ledger.
The Ledger solution is surprisingly elegant and simple. But it isn’t perfect; it has some obvious problems. We are going to look at the two most fundamental ones at the heart of Bitcoin: that a thief can steal money by adding or by modifying the Ledger. The fixes Satoshi proposed for them in 2008 were inspired and ingenious, but nobody at the time could be sure they would work.
Today, we know that they do.
Adding to steal #
The most obvious problem is that an evil player Eve could set up a Game server, get a copy of the Ledger, and then enter into it: “Bob pays Eve 10 Coins; Charles pays Eve 10 Coins; Dana pays Eve 10 Coins”, and so on through the alphabet and beyond. Then her Game server would broadcast this Ledger to the rest of the Game, and all the other Game servers would obediently update their copies of the Ledger with Eve’s changes.
It’s simple for Eve to steal money, simply by adding to the Ledger.
To anyone with a modest knowledge of modern cryptography, the solution is obvious, as Satoshi knew it would be. In his PDF, he stated, without any explanation, that Alice would have to digitally sign the ledger entry. The readers of the cryptography mailing list knew instantly what he meant.
But most likely you don’t; and as a matter of fact, as recently as 50 years or so ago, no one else did either.
The Unthinkable Discovery #
James H. Ellis lay in bed and thought about the unthinkable. A world in upheaval was closing the books on the 60s in this their final year of 1969. A man walked on the moon for the first time, watched by 500 million people on black-and-white television sets. A million more danced at Woodstock, as hundreds of thousands demonstrated against the Vietnam War. In the Cold War, the Soviet Union invaded Czechoslovakia, crushing the Prague Spring with tanks. The first message was sent over the ARPANET, the infant Internet. All in all, it would be a year to remember; and that night, Ellis was to add one more historic event to that remarkable decade’s many. He was about to transform 4,000 years of cryptography; in his words, to show that the unthinkable was actually possible.15
Cryptography is the study of how to send a secret message that only the sender and recipient can read, for example by scrambling its letters in some way. Over the millennia, one fact had remained constant and unquestioned: the sender and the recipient had to share a secret, called the “key”, which could “lock” and “unlock” the secret. Ellis was pondering whether there wasn’t some way around this; it is perhaps easiest to explain his ideas using invisible ink as an analogy.
Imagine that Alice, and only Alice, has a chemical for an invisible ink. This isn’t just any old invisible ink: only one chemical in the world, a different one we’ll call the “reveal” chemical, can make it visible. Alice has made the reveal recipe available to everyone. What Alice keeps secret is the recipe for the invisible ink.
If we apply the “reveal” chemical to a piece of paper and writing appears, it could only have been written by Alice. In effect, Alice can sign documents with this ink, and while no one can forge her signature, everyone can verify it.
On the other hand, Alice could keep the “reveal” chemical secret, and publish the invisible ink instead. Now everyone in the world can send Alice secret, invisible messages. Anyone can write them, but Alice and only Alice can read them.
That night in 1969, Ellis suddenly saw how to prove that this was possible mathematically - but only in the abstract.16 Ellis worked for British intelligence, and he circulated his proof among its secret codebreakers. For years, they tried to find a mathematical formula that would work like invisible ink. Finally, in 1973, one of them named Clifford Cocks finally discovered it. Sadly, the British never did anything with his invention, and all of these events languished in secrecy until 1997.
In 1977, three academics at MIT rediscovered Cocks’ formula, which they named RSA - their last names’ initials. They went on to found a company of the same name, and to transform cryptography and the world of electronic commerce. Today, every Web browser uses RSA to encrypt pages and credit card transactions.17 Without it, the Internet and ecommerce revolutions would be impossible.
The kind of cryptographer that Ellis envisioned, and which Ellis and the three RSA founders invented, is called asymmetric cryptography because, just like requiring two different kinds of ink, it requires two different keys. For digital signatures, the equivalent of the “reveal” chemical is called the public key, and the “hide” or signing chemical’s equivalent is called the private key.
If Alice wants to digitally sign data, like a file, she can use RSA to create a key pair, and put her public key on the Internet for anyone to find. Let’s say she wants to buy a car, and the car dealer emails Alice a PDF with the car loan agreement. To digitally sign the agreement, Alice encrypts the PDF with her private key, and emails the encrypted version back to the car dealer. The car dealer can then get Alice’s public key to decrypt the PDF. If the result is the original car loan, that proves only Alice could have encrypted it, because only Alice has Alice’s private key.
It is as if Alice wrote her signature, in her private invisible ink, on the car loan papers. Then the car dealer brushed the papers with Alice’s public reveal ink, and when Alice’s signature appeared, the car dealer knew only Alice could have put it there – because only Alice has Alice’s private invisible ink.
The Digitally Signed Ledger #
Now we can get back to the first problem we looked at with the Ledger: evil Eve can add fraudulent entries, like “Alice pays Eve 100 coins,” “Bob pays Eve 100 coins,” and so on. The solution Satoshi proposed was one that any amateur cryptographer would think of immediately: require any entry in the Ledger to have the payer’s digital signature. The Ledger would now have two more columns, and a single entry might look something like this:
Figure 4: A digitally signed Ledger entry #
| Payer | Payee | Amount | Date/Time | Payer’s Public Key | Payer Signature |
| Alice | Bob | 100 | 2013 DEC 28 7:32 PM | YReDH2… | aXW8zP… |
The “Payer Signature” column will contain the encryption of all the other columns, encrypted with the payer’s private key. In this example, Alice would encrypt the text: (Alice, Bob, 100, 2013 DEC 28 7:32 PM, YReDH2…) with her private key, and put the result in the last column. This “signature” will just be a long, random looking jumble of numbers and letters, which I’ve represented as aXW8zP….
Any Game server, and any person for that matter, can take Alice’s public key from the “Payer’s Public Key” column, and use it to decrypt aXW8zP…. If the result is (Alice, Eve, 100, 2014 FEB 3 10:22AM, YReDH2…), we say that Alice digitally signed the statement: “Alice, whose public key is YReDH2…, paid Eve 100 Coins on December 28th, 2013, at 10:22 AM.” More importantly, a Game server will only add a transaction to the Ledger if the transaction is digitally signed in this way.
And now, evil Eve can no longer add fraudulent entries to the Ledger like “Alice pays Eve 100 coins.” Eve has Alice’s public key, as does everyone else — it’s a public key, after all — but she doesn’t have Alice’s private key. So if Eve wants to ask a Game server to update the Ledger with a fraudulent entry that says “Alice paid Eve 100 Coins,” Eve can get as far as: (Alice, Eve, 100, 2014 FEB 3 10:22AM, YReDH2…). What Eve can’t do is give the Game server the last column, the “Payer Signature” column. Eve can’t fake Alice’s digital signature. She’s stuck. With digital signatures, we’ve solved the first problem of the Ledger: we’ve made it impossible for anyone like evil Eve to add fraudulent transactions to the Ledger.18
Modifying to Steal #
Imagine one wintry evening while Eve and Bob are playing the Game, Eve pays Bob 1,000 Coins for a unicorn. Time passes. Winter turns into spring, spring into summer, and one balmy day in the fall Eve quietly goes into the Ledger and changes the number 1,000 to 1. Her Game server dutifully broadcasts the change to all the other Game servers, which all update their Ledgers with the change.
If Bob is very wealthy, he may never even notice that Eve stole 999 Coins from him. If he notices that he’s suddenly 999 Coins short, he may have a hard time figuring out which of his many transactions in the Ledger has been changed; he may not have made a backup. And even if he does figure out that it was that winter unicorn transaction, how can he prove that Eve made the change, or that anything is even wrong?
As things stand with the Ledger so far, he can’t. Our new problem is that Eve can steal money not by adding to the Ledger, but by modifying or even deleting transactions from it.
Digital signatures can’t prevent Eve from doing this. After she changes the Ledger entry to read 1 Coin instead of 100 Coins, she can just resign it!
This is a difficult problem. To solve it, Satoshi used another cryptographic invention from the 1970s. To understand it, we need to think a little more deeply about something we are already familiar with: the human fingerprint.
How we know who #
Human beings have various ways of telling each other apart. Faces and names are perhaps the most common, and they work well enough most of the time; but they are far from perfect. In many cultures, names change after marriage. Faces change slowly but surely with age. Modern identifiers include DNA and numbers like the United States’ Social Security Number.
In the table below, I have listed eight important properties and the human identifiers that have them. Notice that only one identifier has (almost) all the properties: the human fingerprint.
Figure 5: Properties of common human identifiers #
| # | Property | Fingerprint | Face | SSN | DNA | Name |
| 1 | One-way | ✓ | ||||
| 2 | Avalanche | ✓ | ||||
| 3 | Random | ✓ | ||||
| 4 | Small | ✓ | ✓ | ✓ | ✓ | |
| 5 | Same size | ✓ | ✓ | ✓ | ✓ | ✓ |
| 6 | Invariant | ✓ | ✓ | ✓ | ||
| 7 | Unique | ✓ | ✓ | ✓ | ||
| 8 | Comparable | ✓ | ✓ | ✓ | ✓ |
The One-Way Property #
Hold up one of your fingers for a moment and look at the print - but really look. That print is unique to you; only you have it. However, you are also a person of innumerable different qualities that make you unique; so what else can this fingerprint tell us about you?
The answer is: nothing. A fingerprint cannot tell us a person’s race, whether they are tall or short, fat or thin, blond or dark, happy or sad, the color of their eyes or even anything about their facial features, whether they are young or old (a small print need not belong to a child), sick or healthy, or a man or a woman, or undecided. A person’s fingerprint is unique among billions of other human beings’, and yet it tells us nothing else about that person. Nothing!
All other human identifiers “leak” information. A person’s name can tell us their gender, likely heritage and country of origin. A mugshot speaks volumes: it can reveal a person’s mood, age, gender, hair color, ethnicity, whether they’ve led a rough life or are trying to, and much else besides. A social security number’s size can give us an idea of a person’s age, and the first three numbers originally indicated the state you were born in. DNA is of course the leakiest human identifier of all.
But the fingerprint reveals nothing. This is an astonishing fact. It seems impossible that one feature can somehow condense the staggering number of variable traits that make a person unique, but at the same time betray none of those other features; and yet, it is so. We might say the fingerprint is a “one-way” property of a person. If you have the person, you can easily get his or her fingerprint; but with only the fingerprint, you can’t go in the reverse direction: you cannot find out anything else about them.
The other properties can be summarized as follows:
One-way: we covered that property above.
Uniqueness “in practice”: The chances of two people having the same fingerprints extremely slight. Calculations of how many different fingerprints are possible range from 1011 to 1080;19 the latter figure is also about how many atoms exist in the universe.20 If that last figure is correct, the chances that two people will have the same prints, be alive at the same time and also accused of the same crime, are smaller than of being struck by lightning while simultaneously winning the lottery and being bitten by a shark. (But see #8 below, and Appendix 3.)
Avalanche effect: Although some twins can have similar fingerprints,21 in general people who differ only slightly in appearance or even DNA from each other have completely different fingerprints. It’s as if a slight difference triggers an “avalanche” of fingerprint changes.
Invariance: although fingerprints can change in children, the fingerprint pattern does not change with age (barring external events like scarring, abrasion, etc).
Small: They are conveniently small, unlike (say) the face.
Same size: Fingerprints are all about the same size; their size varies less between people than height, weight, and so on.
They are essentially random. If you are given all the other visible features of an individual, and even invisible features like their DNA sequence, you can infer exactly nothing about what their fingerprint will look like. Fingerprints are unpredictable and, in that sense, random.
Comparable: unlike Social Security numbers or DNA, fingerprints cannot be compared precisely or easily. Too many false criminal convictions have resulted from this poorly understood fact. Although it doesn’t have much to do with Bitcoin, I felt it important enough to explain in more detail in Appendix 3.
To reveal everything and nothing: the human fingerprint #
So the human fingerprint has all of these eight properties except the last one. In the digital world, the world of files — Microsoft Word files, music and video files, web pages, and so on — there is an equivalent, highly mathematical “fingerprint”. But to understand it, you don’t need to know any mathematics. All you need to know is what properties it has, and those turn out to be exactly the same as the human fingerprint, plus the last property of being comparable.
When specialized words are absorbed into everyday language, they may distort the original meaning. To computer enthusiasts, the term “hacker” originally meant someone who makes anodyne and inventive changes to computer programs and hardware. In everyday English and many other languages, the word has sadly come to mean a computer criminal.
Something like this will happen with the digital fingerprint. You may be about to hear it here first, but for your children and theirs this new word will become boringly commonplace, simply because ever more of our digital lives are impossible without it. That word is “hash”.
The Hash #
“Hash” is a general term in computer science; only the so-called cryptographic hash is an identifier of data that, that like the human fingerprint, has all the properties I listed earlier (and a few more that I did not). An example of data is any sequence of letters and numbers and symbols, like the text you are reading now. In fact, though, any kind of data - the ones in zeros in digital music and movies, for example - can have a hash.
Cryptographic hashes are very difficult to create; even now, over thirty years after the first one was invented, only a handful are in current use. In 1993, the United States government’s National Institute of Standards and Technology (NIST) proposed what is now called SHA-0, the Secure Hash Algorithm. It was quickly adopted throughout the world, and almost as quickly found to not have all of the above properties after all - it wasn’t secure. In part this was due to the stunning pace at which computers kept getting faster and better. We are now up to SHA-3.22
I predict that people will start saying “hash” when they ought to say “cryptographic hash,” just as the meaning of “hacker” changed after it was absorbed into everyday language. It is, or will be, both a noun and a verb: you hash data, and the result is a hash.
Here is the SHA-256 cryptographic hash, an earlier but still widely used SHA, of the letter “h”:
- aaa9402664f1a41f40ebbc52c9993eb66aeb366602958fdfaa283b71e64db123
Here is the SHA-256 hash of a tiny variation, the letter h with a space after it:
- 17c76396f75dbc3aeb8831762248357f0839a12ebd90a1f87c12e95facc7c11b
And here is the SHA-256 hash of the entire text of Leo Tolstoy’s epic novel War and Peace:
- d76017bb899e9ac703f1340acf116fe0bae974f0a5d8cb91c3e43745bb29b3d2
But don’t take my word for it. You can generate these hashes yourself in a fraction of a second. I used a hash generator website I found by Googling “upload file hash generator,” and I downloaded War and Peace from a link on the Gutenberg Project’s website. You can too.
Cryptographic hashes like SHA-256 have all of the properties of a human fingerprint, plus the all-important one of being easy to compare accurately:
Uniqueness “in practice”: The chances of finding any two different texts that have the same hash is nonzero, but infinitesimal; for almost all practical purposes, it can be treated as zero, and is.
One-wayness: They reveal nothing about their original data; they do not “leak”. You cannot tell from looking at a hash whether it is of “War and Peace” or the letter “h”, or anything else. (Hashes are sometimes called “one-way functions.”)
Avalanche effect: Hashes of similar things are in no way similar; note the difference between the hashes of “h” and “h “ above.
Invariance: you can hash War and Peace as many times as you like with, say, SHA-256, and the result will always be the same.
Small: They are conveniently small. A SHA-256 hash can be represented by 64 numbers and letters.
Same size: They are all the same size. For example, every SHA-256 hash can always be represented as a sequence of 64 letters and numbers.
They are essentially random. No matter how much additional data you have about some text — how many vowels and consonants and letters it has, its font, its language — you cannot predict what its hash will be. There is only one way to find out: actually hash it.
Comparability: hashes are drop-dead easy to compare. They are just a string of letters and numbers, and are all the same length. If one letter or number is different, so are the hashes. If they are similar, that means nothing, thanks to the avalanche effect and one-wayness properties.
Uses #
To get an idea of what hashes are good for, imagine that Leo Tolstoy is finishing up War and Peace today on his word processor, and that he is also a bit paranoid. Our Leo suspects that someone is creeping into his house at night, opening the War and Piece manuscript in Microsoft Word, and making little changes to it. But how can Leo be sure? War and Peace is vast; even Leo can’t read through it every morning to check whether a word here and there has been changed.
Our modern Leo Tolstoy can solve his problem with a cryptographic hash. Every night before he goes to bed, he can generate a SHA-256 hash of the manuscript exactly like I did above; print the hash, and put it under his pillow. The next morning when he gets up, he can generate the hash again, and compare it to what is under his pillow. If the two hashes are the same, nobody touched the manuscript!
For an example closer to home, consider a problem Netflix has. Netflix needs to be sure none of their movie files are corrupted, but they can’t pay people to sit around all day watching Netflix’s vast store of movies to see if the sound or picture is suddenly getting garbled in scene 23. Instead, Netflix regularly rehashes each movie, to see if its hash has changed. A computer can do that in almost no time at all.
Satoshi’s solution to the Ledger modification problem was inspired, and it relied crucially on hashes. It was here that he had what we might call the first of his three Grand Ideas. All are at the heart of Bitcoin: if you understand them, you understand how Bitcoin works.
Everything else is just a footnote.
Proof of work #
May 3rd, 1978 dawned dry and clear in Los Angeles, as always. There wasn’t much in the news. A few days earlier, Naomi Uemura had become the first man to reach the North Pole alone, with a team of Malamute sled dogs. Mick Jagger’s marriage was ending, with Bianca Jagger filing for divorce over his affair with the model Gerry Hall. And in the early hours of that morning, a salesman named Gary Thuerk sent a new kind of email message he had been working on for days. It had been a lot of work, but in the end he and his assistant programmer botched it.
Thuerk had painstakingly culled about 300 email addresses from a printed list of 2600, trying to pick out ones located in California. When he finally typed them all into the “to” field, he didn’t know what he was doing. Email at the time had a maximum character limit for that field, and when he finally sent his email, over a hundred of the addresses spilled over into the “subject” and body. The subject of the email was supposed to be: “DIGITAL WILL BE GIVING A PRODUCT PRESENTATION OF THE NEWEST MEMBERS OF THE DECSYSTEM-20 FAMILY”.
It was the first known spam email ever sent, and the reaction was one of fury. The Internet, or Arpanet as it was then known to its 2600 members, has never been the same since.23
In the decades that followed, an enormous amount of effort went into finding technical solutions to fighting spam; as we know, almost all of them failed. (Google’s Gmail seems to have had the most success, but the methods Google uses are understandably a secret.) One idea which seemed promising at the time was proposed by a British cryptographer named Alan Back in 1997, and it used digital fingerprints — cryptographic hashes.
Back’s idea was to slow down a hash, and require every email to include it. Whenever you received an email, your email program would have to compute its hash. If that took about a second, you wouldn’t notice or even care. Spammers can send thousands of emails a second. If they had to compute a unique hash for each one, a thousand emails would instead take almost two minutes; a hundred million would take over three years. Spam would become impractical, and die.
Back didn’t try to invent a new hash that was slow; he knew all too well how difficult cryptographic hashes were to develop, and how few good ones actually existed. Instead, he invented a way to slow down any cryptographic hash by as much or as little as you wanted; it worked like this.
Hashes are essentially random number generators. If you hash an email, you get a number. In the sense that the number is unpredictable, it is random. However, that number will always be between 0 and a (very large) maximum. Let’s say that maximum number is 347,378,779,115,208, which is 15 digits long. If you now require that your hash have 14 leading zeros, there are only ten possible values: 000,000,000,000,000; 000,000,000,000,001; 000,000,000,000,002; and so on, up to 9. Back realized that because hashes are random, if you had to find some text - any text - which hashed to one of these ten numbers, it would be like playing the lottery with odds of 10 to 347,378,779,115,208. It would take you a long, long time. If the requirement was that the hash have only one leading zero, that wouldn’t take long at all: the odds would be 10,000,000,000,000 in 347,378,779,115,208, or about 10 in 347.
Back’s idea was to give everyone who wanted to send an email a challenge: find a number which, when appended to the email and its address, hashes to any number with, say, 12 leading zeros.
For example, if you want to send an email to joe@yahoo.com that just said “Hello Joe”, you first use SHA-256 to hash “0 joe@yahoo.com Hello Joe”. If that hash doesn’t start with 12 zeros, you try next with 1: “1 joe@yahoo.com Hello Joe”. Then with 2, 3, and so on, until you got a hash beginning with 12 zeros. This number that you keep changing is called a “nonce”, which is an abbreviation of “number only once.” Because cryptographic hashes are random, trying to find the nonce is exactly like trying to win the lottery. Instead of buying tickets, you keep trying new nonces. It may take a while, but if you buy enough tickets, you will eventually win.
Once you’ve found the “winning” nonce, you send Joe his email, and include the nonce. When Joe’s email program – say, Microsoft Outlook – receives it, it hashes the nonce and the email with SHA-256. If the result has 12 leading zeros, Outlook puts it in Joe’s Inbox; if it doesn’t, Outlook puts it in Joe’s spam folder. Hashes like SHA-256 are very fast, so it would take Outlook only a fraction of a second to calculate the hash.
Back called his idea “Hashcash” because it would take a spammer time to find the nonce, and time is money (“cash”); and because his invention used hashes. What was ingenious about Hashcash was that it could be easily adjusted. If computers got so fast that spamming became possible again, all you had to do was increase the number of leading zeros to slow spammers down again.
Hashcash failed. Spammers eventually learned how to infect millions of computers using viruses, to create networks called “botnets” (as in, robot network). Criminal spam gangs routinely rent them, to make all the computers send spam. In the obscure cryptography literature, Hashcash lived on as interesting oddity, and was called “proof of work”: having the nonce was proof that you had done the time-consuming work to find it. Hashcash was forgotten.
Or almost forgotten. Ten years later, one person who remembered it was Satoshi Nakamoto. His first Grand Idea, which he presumably had in 2008, was to realize how to use Hashcash to prevent Eve from corrupting the Ledger.
In effect, Hashcash made Bitcoin possible.
Work proofing the Ledger #
To see how Satoshi used Hashcash in Bitcoin, I’m going to oversimplify a little from now on. However, I set the record straight in Appendix 1: Loose Ends, where I fill in some missing details and correct some simplifications. (You don’t really have to read that Appendix though if you just want to understand the principles behind Bitcoin.)
We’re going to change the Game one last time. To pay Bob 1,000 Coins, Eve will send a specially formatted email to any running Game program. The email will look like this:
Figure 6: Eve’s email paying Bob 1000 Coins #
From: eve@evil.com
To: bob@honest.com
Subject: Payment for Unicorn
| # | Field | Value |
| 1 | Payer: | eve@evil.com |
| 2 | Payee: | bob@honest.com |
| 3 | Amount: | 1000 |
| 4 | Date: | 4 JAN 2013 9:59PM |
| 5 | Payer Public Key: | 6KvGUgQugupJfEow6h3E2jjT3XhP7N |
| 6 | Payer Signature: | W8EU6jTQVJtdkM23cx2xaDGzzBxZ3d |
| 7 | Previous Entry’s Hash: | 000000000000ee1e984cc08e93366dc07e81f4e67b720394bf3f6f99d09354f4 |
| 8 | Nonce: | 618,202,206,722,430,347 |
| 9 | Hash: | 000000000000c4bab1d41b401181da505a7fcdb4875ae4be8b0615c1b334ebaf |
| 10 | Nonce minutes: | 10:42 |
We’re already familiar with everything down to the “Payer Signature”, fields 1 through 6. The field below that, “Previous Entry’s Hash”, is the hash of the last entry already in the Ledger. Field 9, “Hash”, is a hash of all the previous fields taken together. It must have a certain number of leading zeros; in this example, twelve zeros. To get that hash Eve will have to have tried out 618,202,206,722,430,346 nonces; the winning one in field 8, 618,202,206,722,430,347, got her a hash with twelve zeros. In this example, it took her 10 minutes and 42 seconds to find that nonce, so in field 10 she put: 10:42.
When the email arrives at a Game server, the Game server will perform a SHA-256 hash of fields 1 through 8. If the result is what is in field 9, the Game server will add the entry to the Ledger. If it isn’t, it won’t, and it will send eve@evil.com a polite rejection notice.
If Eve’s entry does get added to the Ledger, the Ledger will then look something like the figure below. I’ve abbreviated the nonces, hashes, keys, and signatures with ellipsis (…) so that they will fit.
Figure 7: The Ledger with three extra columns: a hash, a nonce, and the time to find the nonce #
| ROW | PAYER | PAYEE | AMOUNT | DATE | PAYER PUBKEY | PAYEE SIG | NONCE | HASH | NONCE MINUTES |
| … | |||||||||
| 213 | Dan | Hal | 73 | 4 JAN 2013 9:57PM | Mjg8y… | xIuJJ… | 343… | 000…354f4 | 9:23 |
| 214 | Eve | Bob | 1000 | 4 JAN 2013 9:59PM | lUMKo… | s17Ta… | 618… | 000…4ebaf | 10:42 |
| … | |||||||||
| 10176 | Gil | Sue | 249 | 7 OCT 2013 2:04PM | shTeb… | 8fis1… | 761… | 000…aW8hU | 8:14 |
| 10177 | Al | Kris | 1000 | 7 OCT 2013 2:05PM | oc2pI… | f7ej9… | 984… | 000…yeD4h | 9:47 |
| … |
All the rows in the Ledger are now chained together, because each row’s hash includes the previous row’s.
And now, Eve has a serious problem. If she wants to change the amount in row 214 from 1,000 Coins to 1 Coin, she will have to recalculate all the hashes for the all the rows that come after it. This is because every row’s hash includes the hash of the previous row. The problem is, for every such row, Eve is going to have to find a new nonce as well; and that will take her about ten minutes per row. But unfortunately for Eve, players all over the Game are constantly adding new rows to the Ledger: it’s a very active Game. Every few seconds a new row is being added to the Ledger. After every ten minutes that it takes Eve to recalculate just one hash, hundreds or thousands more have been added to the Ledger. She’ll never keep up. And that is how Hashcash prevents thieves like Eve from trying to steal by modifying the Ledger.
Of course, Eve could go out and rent a botnet to do all this work for her, but there are two main reasons that is unlikely. First of all, botnets cost money; in fact, they aren’t even cheap. Eve has to ask herself just how much she is willing to spend, in order to cheat on just one transaction in the Ledger: is she really going to be able to make a net profit? It’s pretty unlikely. And secondly, let’s not forget that this is all for a Game. It would be pretty pathetic if Eve were actually willing to spend a lot of real money to cheat someone out of a few Game Coins.
But what if it wasn’t a game?
Game over #
Thus far in our story, the only reason people will be willing to add entries to the Ledger is because they want to play the Game. If there’s no Game, there’s no motivation to go to all this trouble with hashes, digital signatures, and the rest of it. Take away the Game, and everything just stops.
That was Satoshi’s problem. First, he’d had the clever idea of using a Ledger instead of digital pieces of money. Then he figured out how to decentralize it completely, like Bittorrent, by solving the two main problems of theft: he figured out how to use digital signatures and the Hashcash invention to prevent thieves from adding to or modifying the Ledger, without any central authority. The last big conceptual problem he faced was: why would anyone bother?
It was here that Satoshi had what I will call his second and third Grand Ideas. He thought of two ways to motivate people to take part. The main problem was that finding a Hashcash nonce was not only hard, it was actually somewhat expensive: real computers had to spend real time trying out possible nonces, and they had to be powered by real electricity, and cooled with real air-conditioning or fans, all of which had to be paid with real money. Unless there was some kind of reward, like the somewhat frivolous one of being able to keep an online Game going, there was actually a real disincentive for anyone to do anything.
So Satoshi came up with two incentives. The first was that every time you found a nonce, you would be allowed to allocate to yourself some new Bitcoins, out of thin air. They would have been earned.
The second incentive was that every time someone wanted to add a transaction to the Ledger, they could include a “transaction fee” that whoever found the nonce could keep. Think of this as a tip in advance of, instead of after, services rendered.
A typical transaction would go something like this. Let’s say Alice wants to pay Bob 150 Bitcoins. She creates an email like the one in the figure above, and emails it to a Bitcoin program. The server sends it all around the network, eventually reaching every running Bitcoin program.
People called “miners” are constantly monitoring the network for transactions like Alice’s, which want to be added to the Ledger. Miners will prefer transactions with larger transaction fees; they’ll process those sooner than other transactions.
When a miner finds a transaction, she will start looking for a nonce. Of course, multiple miners will often be working on the same transaction; in effect, they are racing each other to see who finds a nonce first. When the finder finds a nonce, she gives it and the transaction to any Bitcoin server running nearby. The Bitcoin server checks that hashing the transaction and the supplied nonce actually produces the alleged hash with leading zeros. If it does, the Bitcoin server updates its copy of the Ledger, and broadcasts it to all the other Bitcoin servers.
Zero to Hero #
So how many leading zeros should a Bitcoin transaction’s hash have? Satoshi had another excellent idea here. Since every transaction includes how long it took to find the nonce, every miner starts by calculating the average time it took in the past two weeks. If that average sinks below ten minutes, which of course it will as computers continue to get better and faster, a Bitcoin formula determines how many zeros must be added to bring the average up to ten minutes. If the average rises above ten minutes, maybe because of a world war or some other disaster, the number of required zeros is decreased. Every miner and every Bitcoin server has the formula for determining the number of zeros.
Changing the World: A Summary #
On October 30th, 2008, when Satoshi sent his seminal email to the mozdev.com mailing list, he was proposing something utterly preposterous: a world-wide, stable, digital currency powered entirely by the participants of a network, without any central authority. At the core of his proposal were five key ideas:
Use a single Ledger as a digital currency.
Use digital signatures to prevent people from adding fraudulent entries to the Ledger.
Use the Hashcash principle to prevent people from fraudulently modifying the Ledger.
Reward “miners” for finding nonces by allowing them to digitally “mint” a certain number of Bitcoins for themselves.
Reward “miners” for finding nonces by allowing them to collect voluntary transaction fees from each transaction.
Would it work? In the month that followed, powerful arguments for and against flew back and forth on the mailing list, with Satoshi doing his best to defend his idea and finish the computer code that would implement it. But everyone knew there was really only one way to find out: try it.
Today we know only one thing for certain: it has worked for the last six years or so.
Will it continue to work? I don’t know, and neither does anyone else. Great things have been promised if it does, and the chances are that you found your way to this essay because you have read some of those promises. I can’t tell you whether Bitcoin will be around for another year, or century, or millennium. I don’t want to speculate on how it may benefit or imperil mankind; much wiser writers have already done that, and will continue to. The only thing I can tell you is, at least in principle, how Bitcoin works.
If I’ve succeeded, you now know.
Appendix 1: Loose Ends #
As I said in the beginning, I have to some extent simplified and distorted how Bitcoin actually works, in order to explain it more clearly. In this section, I tie up those loose ends by correcting those over-simplifications.
Ledgers, Blocks, Chains, and Miners #
Miners don’t mine one transaction at a time. Instead, they scan the network for large groups of them called “blocks”. They prefer to include transactions with larger transaction fees, so if you want your transaction processed sooner rather than later, you’ll want to increase your transaction fee accordingly. When they’ve collected enough transactions for a “block”, they start searching for a nonce to hash the entire block, not each of its transactions. They don’t use the hash of the last transaction in the Ledger, but the hash of the last block.
They are racing against each other, and they don’t all have the same transactions in their blocks. Whoever finds a nonce first quickly adds it to the Ledger. As the Ledger’s changes get broadcast around the network, the other Miners find out that they’ve lost that race, discard their blocks, and start work on a new one.
What I’ve called “the Ledger” is called the “blockchain” in Bitcoin, because it’s a chain of blocks.
What’s rather beautiful is that the more miners and transactions there are, the harder it is for an evil Eve to to try to undermine the system – even if every participant in the network is an evil demon, determined to cheat everyone else. That’s the opposite of a centralized system, which becomes weaker the more transactions and financial participants it has to coordinate.
Also, for various reasons, Satoshi designed Bitcoin so that the Bitcoin reward for finding a nonce decreases steadily over time. Eventually, perhaps around 2040 or so, no more new Bitcoins will be generated, and from then on, miners’ only incentive will be transaction fees. Will Bitcoin still work? Will miners still be motivated to mine? That remains to be seen.
Anonymity #
The Ledger has columns similar to the ones I used in my examples, but the Payer and Payee columns don’t contain names like “Alice” or “Bob”. Instead, they contain public keys. A public key can optionally contain an email address or other information; that does, after all, make it easier for other people to contact you - to buy something from you, for example.
Does that make Bitcoin as anonymous as cash? The answer is: it depends. Mostly it depends on how careful and technically savvy a Bitcoin user is. To illustrate this, consider the example of the bomb threat that was emailed to Harvard University in December, 2013. Harvard quickly evacuated and searched four buildings, and although no bombs were found, the FBI immediately began a search for the culprit.
The email itself was anonymous; it had come from a server that allows anyone to create an email address without providing any further identifying information. However, the route the email had taken showed that the sender had logged in from the Tor network. Tor is a network maintained by volunteers that uses cryptography to help people browse the Internet anonymously. It is used a good deal by private citizens in Iran, for example, where visits to many websites can get you arrested and even executed. With Tor, governments and their intelligence agencies, or anyone else for that matter, can see who goes in to the network, and who comes out. So Iranian intelligence can see that hundreds or thousands of Tor users, “coming out of” Tor, are visiting dissident or irreligious websites; and they can also see that hundreds or thousands of Iranian computers, and thousands of other computers around the world, are simultaneously logged into Tor. What they can’t do is connect the two: Tor prevents them from figuring out which of the thousands of Tor users is actually browsing apostasy.com or whatever. Is it that well-known dissident they’ve been monitoring for months who is logged into Tor right now, or is it a teenager in Argentina who is also logged into Tor? No one knows.
So the FBI asked Harvard’s network administrators whether anyone had been logged into Tor from the Harvard network around the time that the email was sent; in fact, only four Harvard computers had been. One of them was in a dorm room. So the FBI went to the dorm, knocked on the door, and confronted who was inside. It was an undergraduate who quickly confessed that he had staged the whole incident to get out of an exam he was afraid of failing.
When people ask me whether Bitcoin is anonymous, I think of this incident. That Harvard student knew how to acquire a completely anonymous email address, but he didn’t know how to use it. Bitcoin is anonymous in this way: if you know what you’re doing, and are very careful, you can be pretty successful at covering your tracks. But you still have to worry about transactions with people who aren’t anonymous, and the FBI or Interpol following a chain of other peoples’ “leaky” transactions that lead them to your dorm room door too.
Many people, and especially governments, will argue that this makes Bitcoin so dangerous that it should be made illegal. I’ve avoided giving my opinions everywhere else in this essay, but I want to share two of them here. First, cold hard cash is also anonymous: if anything, it’s harder to trace where a one hundred dollar bill came from than a public key. Second, police work is only easy in a police state; in a democratic and free society, it’s supposed to be hard.24 That’s part of the point of protecting citizens from government excesses. Well, that’s just my opinion; use it as you wish.
Wallets #
You’ve probably read about Bitcoin wallets. If there are no actual Bitcoin coins, what is a wallet for?
It’s for your private key. If you want to pay someone with Bitcoins, you have to digitally sign that transaction, or it won’t be added to the Ledger. People can pay you all day long, using your public key as the “payee” address, and your Bitcoin millions can pile up that way. But if you don’t have a private key, or lose it, you can never pay anyone. You’ll be wealthy and broke at the same time!
“Wallet” has come to be a very general term for software or even hardware for storing a private key. But a private key is just a very long number. You could print it out if you wanted to, and stick the paper in your leather wallet; some people do. Other people trust their private keys to online websites. That’s a mistake the depositors of [Mt.Gox][http://www.dailytech.com/Inside+the+MegaHack+of+Bitcoin+the+Full+Story/article21942.htm] made; that website turned out to have lousy security, and the keys were stolen. (One of Mt. Gox’s security flaws, by the way, was that they were using a flawed and outdated cryptographic hash, MD5, to store their users’ logins and passwords (not for the Bitcoin Ledger).)
Mining #
Mining has become a competitive business. An interesting aspect of mining is that it is highly “parallelizable”; in other words, it is easy to have multiple computers mining at the same time. All you have to do is give the first computer the task of testing nonces from 1 to 100,000; the second, from 100,001 to 200,000; and so on. Computer graphics cards are designed to work this way, so Bitcoin miners like to use them.
As I said, it costs money to rent a botnet; and of course, you have to deal with dangerous criminals as well. There was an interesting case of a company that successfully sold a computer game that was actually designed to surreptitiously use the gamer’s computer to mine for Bitcoins. The company was caught because some users’ computers overheated and were damaged. Writing a successful computer game is certainly a safer way to get a botnet than dealing with Internet mobsters, but it is still illegal.
Alternatively, many web sites will pay you in Bitcoins if you allow them to use your computer to mine. It’s like buying stock in a company; instead, everyone does a little bit of the mining, and the proceeds are split among all the participants.
The famous Silkroad used a combination of this approach and Tor to hide its transactions from the law. Just as with Tor, the FBI could see that a lot of people in America were making Bitcoin payments to Silkroad, and that a lot of drug peddlers overseas were getting Bitcoin payments from the Silkroad. What they couldn’t do was figure out who was paying whom. They finally took down the Silkroad because the twenty-something programmer running it did something as dumb as the Harvard undergrad: he accidentally left his real email address somewhere on the web, and also ordered fake IDs from Canada to be shipped to his physical address. The FBI stormed him while he was sitting in a library, before he could close his encrypted laptop; that’s how they got access to the Silkroad’s records, and could finally unravel who was paying whom for which drugs.
Appendix 2: Alice buys a washing machine from Bob for 100 Bitcoins #
The table below illustrates the use of digital signatures by showing two versions of the same conversation side by side. In the first conversation, in the first column, Alice uses her private and public keys and a digital Bitcoin ledger (which I call the Ledger) to buy a washing machine from Bob. Imagine that Alice has walked into Bob’s shop after seeing the washing machine in his shop window.
This first version could actually happen in the real world. The second couldn’t, but many readers may find it easier to understand.
In the second, almost identical version, Alice uses her invisible and “reveal” ink, and a paper Ledger, to buy the washing machine. Alice’s Bitcoins are recorded in a paper Ledger, which Bob has a copy of. Every time she paid someone Bitcoins in the past, Alice signed that entry in the paper Ledger with her invisible ink. She just wrote “Alice” in her invisible ink, in the “Payer Signature” column.
| Step | Digital signature & digital ledger conversation | Invisible ink and paper ledger conversation |
| 1 | Alice: Hello, I would like to buy the washing machine you have listed for 100 Bitcoins. | Alice: Hello, I would like to buy the washing machine you have listed for 100 Bitcoins. |
| 2 | Bob: We have a few of those left. What is your public key please? | Bob: We have a few of those left. What is your name and the formula for your “reveal” ink please? |
| 3 | Alice: My public key is ab5WRv… . | Alice: I’m Alice, and my reveal ink recipe is: two parts starch, one part sodium nitrate, and ten parts water. |
| 4 | Bob: Thank you. One moment please while I check the Ledger to make sure that public key has enough Bitcoins for this transaction. | Bob: Thank you. One moment please while I mix those ingredients, and then check the paper Ledger to make sure you have enough Bitcoins for this transaction. |
| 5 | Bob: Thank you for waiting. I have checked the Ledger, and I see that this public key does indeed have more than 100 Bitcoins. | Bob: Thank you for waiting. I’ve checked the paper Ledger. That reveal ink formula does indeed cause the signature to be visible for all entries for Alice; and furthermore, this Alice also has more than 100 Bitcoins. |
| 6 | Bob: I now need you to prove that you are indeed “Alice;” or rather, that you possess the private key that corresponds to the public key you gave me, ab5WRv… . | Bob: I now need you to prove that you are indeed Alice; or rather, that you have the invisible ink that goes with the “reveal” ink you gave me. |
| Bob (continued): I’m going to email you a random sequence I just made up: ilikechocolate. Please encrypt it with your private key, and send me the result. | Bob (continued): Here is a blank piece of paper. Please write the following on it in your secret invisible ink: ilikechocolate. | |
| 7 | Alice: Here you go: I’ve encrypted it, and you’ll see in your email that the result is e3654e. | Alice: Here you go: I’ve written ilikechocolate in my invisible ink on the paper. |
| 8 | Bob: Thank you. One moment while I decrypt that with the public key ab5WRv you gave me earlier. | Bob: Thank you. One moment while I swab the paper with the “reveal” mixture you gave me earlier. |
| 9 | Bob: Excellent: the result is ilikechocolate. This proves you have the private key that corresponds to the public key ab5WRv. | Bob: Excellent: the writing ilikechocolate became visible for a few seconds. This proves you have the corresponding invisible ink. |
| Bob (continued): And, as I said a moment ago, the Ledger shows this public key has more than 100 Bitcoins. | Bob (continued): And, as I said a moment ago, the paper Ledger shows that the owner of this invisible ink has more than 100 Bitcoins. | |
| Bob (continued): So I will now sell you the washing machine. Why? Because you, and only you, can sign a new entry in the Ledger “Alice pays Bob,” and you’ve proven that you have the private key to do it with. | Bob (continued): So I will now sell you the washing machine. Why? Because you, and only you, can sign a new entry in the Ledger “Alice pays Bob” in invisible ink, and you’ve proven you have that invisible ink. |
Appendix 3: Brandon Mayfield’s Fingerprints #
It was Wednesday, and after five days of excitement FBI agent Terry Green was proud of himself.25 Over the weekend a dozen or so images of fingerprints had been emailed from Spain, and Green had run them through three FBI databases; each database returned 20 possible matches, or 60 per print. Green had manually inspected all of them, and with LFP (Latent Finger Print) 17, he had struck gold. As the FBI would later write in its affidavit for an arrest, it was a “100% match” that had been confirmed by a second expert “with over 30 years of experience”. More reviewers approved the match of the next few days, and soon one Brandon Mayfield and his family in Portland, Oregon were under 24 hour surveillance. Interpol was informed that the FBI had a suspect.
LFP17 wasn’t just any fingerprint. Two weeks earlier, on March 3rd, 2004, ten railway bombs in Madrid had killed nearly 200 people, flinging their body parts into nearby apartments, and had injured almost ten times as many. LFP17 and the other prints had been found on a plastic bag full of detonators later that day, in a stolen van parked outside one of the train stations. The Spanish police still had no good leads.26
Over the next two months LFP17 would be reviewed and confirmed again and again by the FBI. After one of them, prompted by doubts from the Spanish police, an agent excitedly emailed the Portland team: “I spoke with the lab this morning and they are absolutely confident that they have a match on the print. - No doubt about it!!!!! - They will testify in any court you swear them into.” On May 19th a final fingerprint expert, chosen by Mayfield’s own defense counsel from a list of three supplied by the prosecuting US government, also concluded that LFP 17 belonged to Mayfield.
On May 20th, Mayfield was abruptly released; two years later, the FBI gave him two million dollars and an abject letter of apology.
What went wrong?
LFP17 looks like a photograph of Neil Armstrong’s first foot print on the moon, with almost as much rock and not quite so much foot print.27 That’s what most crime scene fingerprints look like. Brandon Mayfield’s prints, which were on file from an arrest when he was a teenager — all charges were dropped — consists of beautifully clear, sharp black lines on a white background. Agent Green and others found over a dozen similarities (the number kept rising over the months) between the main body of LFP 17 and of one of Mayfield’s prints, but dissimilarities between the top left and the bottom. The FBI decided to dismiss these as likely due to overlaps with someone else’s prints.
The Spanish police did not. As they continued to chase down suspects and leads, they stumbled on documents with the name Ouhnane Daoud. The prints of someone with that name turned out to be on file in Spain for an immigration violation — and they matched not only all portions of LFP17, but also two other prints on the same plastic bag that LFP17 came from. (Daoud remains at large to this day.)
Spain informed the FBI of their findings on May 19th. On May 20th, they announced it to the press. This created a sensation around the world, because Brandon Mayfield’s arrest had been headline news for the previous two weeks. Under intense media pressure, he was set free within hours.
The problem here is not that no two people have the same fingerprints. Calculations of how many different fingerprints are possible range from 1011 to 1080;28 the latter figure is also about how many atoms exist in the universe.29 If that last figure is correct, the chances that two people will have the same prints, be alive at the same time and also accused of the same crime, are smaller than of being struck by lightning while simultaneously winning the lottery and being bitten by a shark.
The problem instead is that there is no reliable way to compare fingerprints. To understand why, imagine you are shown two photographs and are asked whether they are of the same adult. One photograph is a sharp mug shot. The other is taken with a telephoto lens from a distance, in low light, in the rain, and the subject is turning away from the camera, so that only part of his (or her) face can be seen.
If the faces and heads in both photographs are similar, there is no scientific way to determine absolutely whether they are of the same person. For example, a computer algorithm could sharpen the bad photo to make it look like the mug shot; but another could sharpen it to make them look different. Absent any further information, there is simply no way to make a precise determination; ultimately, it’s a matter of opinion. The relevant skills are those of an art critic, and art critics are not known for agreeing with each other.
And neither are fingerprint “scientists”. In the days that followed Mayfield’s release, four of the FBI’s top experts, none of whom had been previously involved in the case, “with a combined total of ninety-three years of experience in the latent print science,”30 pored over LFP 17 and the other prints and reached the conclusion that — well, that they just couldn’t agree. That isn’t science, and it is compounded by inevitable institutional weaknesses. As the Inspector General’s report laconically put it two years later, "At this point, miscommunications within the FBI and DOJ (Department of Justice) about the [FBI’s Finger print lab]‘s conclusions and the reasons for the error began to proliferate.”31
There are many reasons that LFP17 was so badly misidentified for so long, and they fall into two broad categories. The first is that the skills required to compare crime scene fingerprints with each other, or with prints carefully made by rolling a person’s inked finger over paper, are the skills of an art critic, not a scientist. No matter how often people refer to “the fingerprint science,” it isn’t one and never will.
The second category of reasons was described in the official report conducted by the United States Department of Justice. It is highlighted by the fact that agent Terry Green was proud of his LFP 17 match. If a justice system is going to use fingerprints to convict people of crimes, nobody in charge of making those fingerprint identifications should ever be allowed to know anything whatsoever about the alleged crime. Terry Green was working on the biggest terrorism case in the world since 9/11. It could make the careers of everyone who worked on it if they could find the criminals behind it. Terry Green knew this, and so did every other expert the FBI paid to look at LFP17. The outside contractors knew it too; in general, if a contractor knows how badly their customer wants a positive identification, he or she will feel pressure to supply it future contracts may well depend on it.
The Inspector General’s report made a number of recommendations in this regard: that fingerprint experts should not be employees of the FBI, to avoid feeling pressure to provide positive results; that the non-FBI fingerprint analysts should not only not know anything about the prints’ cases, but that the FBI should never know which analyst provided which analysis. That way, no fingerprint analysis firm would feel pressure to provide positive results. Furthermore, all requests for fingerprint analysis should include random “control” prints; obviously if an analyst says they match the crime scene print, something is very wrong.
The FBI has said repeatedly that they adopted some of the recommendations, but to my knowledge they have never said which ones, or to what extent they have implemented them. I submitted a detailed request about this to the FBI in March of 2014; I have yet to receive an answer.
-
© 2014 · All Rights Reserved · Richard Bondi, rbondi@gmail.com. How Bitcoin Works: A Guide for the Digitally Perplexed by Richard Bondi is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. ↩
-
The internet archive has a 2012 copy of the page that looks exactly like the one that loaded in January, 2014. ↩
-
See http://en.wikipedia.org/wiki/List_of_largest_daily_changes_in_the_Dow_Jones_Industrial_Average. On September 29th, it would break that record again, dropping over 777 points in a day. ↩
-
See http://www.metzdowd.com/pipermail/cryptography/2008-October/014810.html. ↩
-
A Google date search of the mailing list’s archives for “Satoshi Nakamoto” before October 30th, 2008, yields no results; searching after that date does. See here for how these searches are constructed. ↩
-
Newsweek magazine claimed to have found the real Satoshi Nakamoto in March of 2014. ↩
-
[http://techland.time.com/2011/04/16/online-cash-bitcoin-could-challenge-governments/]. For a brief history of Bitcoin, see https://www.youtube.com/watch?v=0ljx4bbJrYE for a talk by the lead programmer who took over when Satoshi mysteriously retired. There is also a quite detailed, interactive timeline at http://mashable.com/2014/02/10/bitcoin-history/. A note for programmers: the source code was originally hosted at sourceforge.net, but moved to github.com in 2011. ↩
-
For a brief history of Bitcoin, see https://www.youtube.com/watch?v=0ljx4bbJrYE for a talk by the lead programmer who took over when Satoshi mysteriously retired. There is also a, quite, detailed, interactive timeline at http://mashable.com/2014/02/10/bitcoin-history/. A note for programmers: the source code was originally hosted at sourceforge.net, but moved to github.com in 2011. ↩
-
While it doesn’t matter for our story, note that this isn’t how banks actually operate; see http://www.bankofengland.co.uk/publications/Pages/news/2014/051.aspx. ↩
-
For the more technically minded, we should note that this is only true if, for example, the bandwidth is one hundred times greater than the transfer rate of each server, and each server has the same rate. ↩
-
You may have read about the owners of a website in Sweden called The Pirate Bay being prosecuted for illegal Bittorrent downloads. The Pirate Bay is not, and never was, a Bittorrent server; instead, it’s merely a search engine of Bittorrent servers that, for example, lets you find which Bittorrent servers have a copy of a particular movie. If merely publishing which Bittorrent servers have movies sounds like free speech to you, and that no-one should be prosecuted for it, you’re not alone. Then again, if it doesn’t, you’re also not alone. Welcome to the 21st century. ↩
-
https://web.archive.org/web/20030610193721/http://jya.com/ellisdoc.htm, paragraph 7. ↩
-
For a modern account of Ellis’ proof, see http://unscramblings.blogspot.com/2014/03/ellis-proof-of-asymmetric-cryptography.html. ↩
-
For more on the history of RSA, see http://cryptome.org/ukpk-alt.htm. ↩
-
Some readers may find Appendix 2 helpful here. It contains an example of Alice buying a washing machine from Bob using her digital signature. ↩
-
Presentation: On the Uniqueness of Fingerprints by Anil K. Jain, Michigan University. ↩
-
[A Review of the FBI’s Handling of the Brandon Mayfield Case (Unclassified and Redacted), Special Report, March 2006, Office of the Inspector General, p. 33] http://www.justice.gov/oig/special/s0601/PDF_list.htm) ↩
-
The New Yorker, http://www.newyorker.com/archive/2004/08/02/040802fa_fact ↩
-
[A Review of the FBI’s Handling of the Brandon Mayfield Case (Unclassified and Redacted), Special Report, March 2006, Office of the Inspector General, Figure 6A] http://www.justice.gov/oig/special/s0601/PDF_list.htm) ↩
-
Presentation: On the Uniqueness of Fingerprints by Anil K. Jain, Michigan University ↩
-
[A Review of the FBI’s Handling of the Brandon Mayfield Case (Unclassified and Redacted), Special Report, March 2006, Office of the Inspector General, p. 87] http://www.justice.gov/oig/special/s0601/PDF_list.htm). ↩
-
[A Review of the FBI’s Handling of the Brandon Mayfield Case (Unclassified and Redacted), Special Report, March 2006, Office of the Inspector General, p. 98] http://www.justice.gov/oig/special/s0601/PDF_list.htm) ↩